| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- 회귀
- programmers
- gan
- 파이썬
- python3
- 운영체제
- 프로그래머스
- LSTM
- db
- Regression
- Heap
- 정렬
- GIT
- PANDAS
- Seq2Seq
- SQL
- Stack
- Python
- 국민대학교
- C++
- googleapiclient
- 재귀
- 국민대
- 데이터베이스
- kmu
- machine learning
- OS
- 머신 러닝
- 스택
- instaloader
- Today
- Total
정리 노트
퀵 정렬(Quick Sort) (with Lomuto) 본문
이 글은 Divide & Conquer에 대해 기본적인 내용을 알고 계신다는 가정 하에 작성되었습니다. 따라서 분할 정복 기법에 대해 잘 모르시는 분들은 제가 저번에 썼던 글을 참고하셔도 됩니다.
2022.10.17 - [개념 정리/알고리즘] - 분할 정복 기법(Divide & Conquer)
퀵 정렬
이름 그대로 빠르게 정렬하는 알고리즘입니다. 퀵 정렬도 분할 정복 기법 방식으로 설명할 수 있습니다.
- Divide: 배열의 원소들 중 임의의 원소 하나를 기준(pivot)으로 정하고 기준보다 작은 원소들의 그룹과 큰 원소들의 그룹으로 나눕니다.
- Conquer: 기준점을 중심으로 나누어진 두 그룹을 recursive 하게 quick sort를 수행합니다.
이 설명에서는 'combine' 과정이 빠져있습니다. 왜냐 하면 두 단계로 충분히 정렬할 수 있기 때문입니다. 이게 가능한 이유는 divide 단계에서 많은 작업이 이루어지기 때문입니다. 퀵 정렬에서의 divide 과정을 특별히 'partition'이라 부릅니다.
Partition 하는 방법
먼저 pivot으로 삼을 원소를 하나 고릅니다. 기준을 고르는 방법에는 세 가지가 존재합니다.
- 가장 왼쪽에 있는 원소
- Random 하게 선택
- 왼쪽, 중앙, 오른쪽 원소들 중에 중앙값을 선택하고 가장 왼쪽에 있는 원소와 swap
Random 하게 선택을 하는 경우 random 한 숫자를 구하는 시간이 오래 걸린다는 단점이 있습니다. 가장 왼쪽에 있는 원소를 고르는 방법은 구현하기 간단하다는 장점이 있습니다. 마지막 방법은 실제로 구현할 때 많이 사용하는 방법이라고 합니다. 퀵 정렬에서는 이 partition을 어떻게 하느냐에 따라 여러 가지 변형된 알고리즘들이 존재합니다. 이 글에서는 Lomuto라는 사람이 제안한 partition 방법으로 설명드리겠습니다. Lomuto가 제안한 partition은 그냥 가장 왼쪽에 있는 원소를 pivot으로 고르는 것으로부터 시작됩니다.

그림에서 i는 pivot의 위치의 다음 위치에서부터 배열의 끝까지 하나씩 배열의 원소를 살펴보는 인덱스, j는 pivot이 있어야 하는 위치를 가리키는 인덱스라고 합시다. 위 그림은 partition의 진행 과정 중 하나의 순간을 그린 것입니다. i번째 배열의 원소와 pivot을 비교했을 때 작으면 j 값을 하나 늘리고, j번째 원소와 i번째 원소를 swap 합니다. 그 후로 i값을 하나 증가시킵니다.
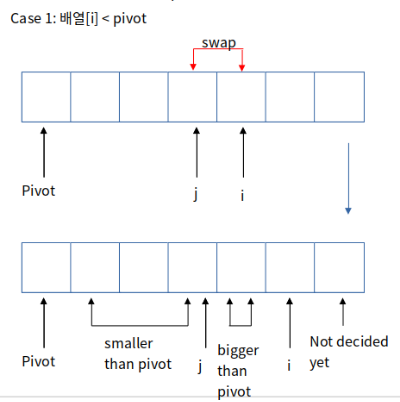
반대로 pivot의 값보다 i번째 원소가 크거나 같으면 i값만 하나 증가시킵니다.

이런 방식으로 i가 배열의 끝까지 탐색을 하면 배열은 최종적으로 아래와 같이 두 그룹으로 나뉩니다.

마지막으로 pivot에 위치한 원소와 j번째 원소를 swapping 시키면 이제 pivot을 기준으로 왼쪽은 pivot보다 작은 값들, 오른쪽은 크거나 같은 값들이 모여있게 됩니다.

이게 partition 과정을 거쳐서 얻은 가장 큰 결론입니다. Partition 과정을 통해 pivot 값이 원래 있어야 할 위치로 옮겨지게 됩니다. 이렇게 partition 과정을 열심히 거친 덕분에 combine 과정은 필요 없어지게 됩니다.
이 과정이 끝나고 양 그룹에 대해 recursive 하게 들어갈 때 이 pivot은 건드리지 않습니다. (배열의 중간 값을 같이 가져갔던 merge sort와 다릅니다.) 이 과정을 c++ 코드로 작성한 것이 아래의 코드입니다.
int partition(int* numArr, int low, int high)
{
/*
numArr: 숫자들이 담긴 배열
low: 배열의 시작점
high: 배열의 끝점
*/
int pivotPos = low; // pivot을 가장 왼쪽 값으로 설정
int pivotValue = *(numArr + low);
for (int i = low + 1; i <= high; i++)
{
if (*(numArr + i) < pivotValue)
{
pivotPos++;
// Swap
int tmp = *(numArr + pivotPos);
*(numArr + pivotPos) = *(numArr + i);
*(numArr + i) = tmp;
}
}
// Swap
int tmp = *(numArr + low);
*(numArr + low) = *(numArr + pivotPos);
*(numArr + pivotPos) = tmp;
return pivotPos;
}퀵 정렬(C++ 코드)
위에서 설명한 partition 과정과 두 그룹에 대해 recursive 하게 들어가는 것까지 구현한 코드입니다.
void quickSort(int* numArr, int start, int end)
{
if (start < end)
{
int pivotPosition = partition(numArr, start, end); // 피벗의 위치
quickSort(numArr, start, pivotPosition - 1);
quickSort(numArr, pivotPosition + 1, end);
}
}Partition 과정과 quickSort 코드를 보면 정렬할 때 배열에 길이에 비례하는 메모리를 추가적으로 필요로 하지 않습니다. 따라서 퀵 정렬은 In-place 알고리즘입니다(메모리 복잡도: O(1)). 그리고 퀵 정렬은 stable 하지 않은 알고리즘입니다.
(2022.10.23 일요일 수정) 예를 들어 길이가 5인 배열 {5, 3, 5*, 2, 6}을 정렬하면 {2, 3, 5*, 5, 6} {3, 2, 1, 2*, 4}를 정렬하면 {1, 2*, 2, 3, 4}가 됩니다.
시간 복잡도
퀵 정렬에서의 base operation은 partition 과정에서 배열의 데이터와 pivot 간의 비교 연산 횟수입니다.
먼저 최악의 경우일 때부터 살펴봅시다. 최악의 경우는 정렬된 배열이 들어오는 경우입니다. 언뜻 생각하면 정렬이 이미 되어있으니 오히려 좋은 것이 아닌가 싶겠지만 생각해보면 아닌 것을 알 수 있습니다.

위의 배열을 보면 partition 후에 정확히 양쪽으로 같은 길이의 배열들이 생성되었습니다. 이에 대해 recursive 하게 들어가게 되면 새로 정하는 pivot에 대해 2번만 비교 연산을 하면 됩니다. 하지만 아래와 같이 한쪽으로 다 쏠리게 되면 recursive 하게 들어갈 때 새로 정해진 pivot과 5번의 비교 연산을 진행하게 됩니다. 따라서 base operation의 진행 횟수를 T(n)이라 할 때, 최악의 경우를 아래의 점화식으로 표현할 수 있습니다.
$$ T(n) = \left\{\begin{matrix}
0\quad(n = 1) \\ T(n - 1) + (n - 1)\quad(n > 1)
\end{matrix}\right. $$
n > 1일 때 n - 1이 더해지는 이유는 partition 과정에서 총 n - 1번의 비교 연산이 이루어지기 때문입니다. 따라서 이 식을 풀어보면,
T(n) = T(n - 1) + (n - 1) = { T(n - 2) + (n - 2) } + (n - 1) = { T(n - 3) + (n - 3) } + (n - 2) + (n - 1) =...
= T(1) + 1 + 2 + ... + (n - 2) + (n - 1) = n(n - 1) / 2
따라서 이를 big-O 표기법으로 표현하면 worst case에 대해 O(n**2) 임을 알 수 있습니다.
이번에는 best case를 점화식으로 표현해보겠습니다.
$$ T(n) = \left\{\begin{matrix}
0\quad(n = 1) \\ T(\left \lceil \frac{n - 1}{2} \right \rceil) + T(\left \lfloor \frac{n - 1}{2} \right \rfloor) + (n - 1)\quad(n > 1)
\end{matrix}\right. $$
이 식을 풀어보면 최종적으로 O(n*log n) 임을 알 수 있습니다. 점화식이 풀어지는 과정은 병합 정렬 때와 같으므로 제가 저번에 썼던 병합 정렬 글의 마지막 부분을 보시면 됩니다.
2022.10.20 - [개념 정리/알고리즘] - 병합 정렬(Merge Sort)
Best case의 경우 pivot 값이 전체 배열의 중간 값으로 잘 설정됐기 때문에 가능하지 실제로는 이렇게 되기 쉽지 않다고 합니다. 평균적인 경우에서의 시간 복잡도는 best case 때와 똑같다고 알려져 있습니다. Quick sort의 경우만 예외적으로 성능을 평가할 때 worst case가 아닌 average case의 경우를 보고 판단합니다.
그러면 여기서 의문이 들 수도 있습니다.
병합 정렬은 O(n*log n)이고 퀵 정렬은 worst case일 때 O(n**2)이면 병합 정렬을 쓰지 왜 퀵 정렬을 쓰지?
실제로 병합 정렬보다 퀵 정렬을 선호하는 사람이 있습니다. 이에 대한 몇 가지 이유가 있습니다.
- 병합 정렬은 In-place 알고리즘이 아니지만 퀵 정렬은 In-place 알고리즘
- 병합 정렬은 combine 과정이 필요하지만 퀵 정렬에서는 그런 거 없음
'개념 정리 > 알고리즘' 카테고리의 다른 글
| 동적 계획법(Dynamic Programming, DP) (0) | 2022.11.02 |
|---|---|
| 퀵 정렬(Quick Sort) (with Hoare) (0) | 2022.10.23 |
| 병합 정렬 그 두 번째 이야기(Merge Sort) (0) | 2022.10.21 |
| 병합 정렬(Merge Sort) (0) | 2022.10.20 |
| 분할 정복 기법(Divide & Conquer) (0) | 2022.10.17 |




