| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- db
- 국민대
- 파이썬
- gan
- python3
- PANDAS
- Python
- GIT
- LSTM
- machine learning
- 데이터베이스
- programmers
- Heap
- 운영체제
- Seq2Seq
- 회귀
- Regression
- 스택
- 프로그래머스
- Stack
- SQL
- instaloader
- 머신 러닝
- 정렬
- 국민대학교
- 재귀
- C++
- OS
- kmu
- googleapiclient
- Today
- Total
정리 노트
로지스틱 회귀(Logistic Regression) 본문
이 포스트는 국민대학교X프로그래머스 주관하는 '2022학년도 여름방학 인공지능 온라인 실전 부트캠프'에서 배운 내용을 정리하는 포스트입니다.
선형 회귀로 분류 문제 해결해보기
저번 글에서 선형 회귀에 대해 알아보았습니다.
2022.08.01 - [개념 정리] - 선형 회귀(Linear Regression)
선형 회귀(Linear Regression)
이 포스트는 국민대학교X프로그래머스 주관하는 '2022학년도 여름방학 인공지능 온라인 실전 부트캠프'에서 배운 내용을 정리하는 포스트입니다. 회귀? 회귀는 특정 데이터가 주어졌을 때 결과
study-note-99.tistory.com
선형 회귀로 분류 문제를 풀어보도록 하겠습니다. 먼저 사용할 데이터는 아래와 같습니다.
| 입력 숫자(자연수) | 성공 여부(1: 성공, 0: 실패) |
| 1 | 0 |
| 2 | 0 |
| 3 | 0 |
| 4 | 1 |
| 5 | 1 |
| 6 | 1 |
가설 함수로 H(x) = x(W=1, b=0)이라고 생각하고 선형 회귀 모델에 따라 학습을 하면 아래와 같은 결과를 얻습니다.

선형 회귀의 결과 중 1을 넘어서는 값도 있기 때문에 분류하는 문제에서는 선형 회귀가 적합하지 않음을 볼 수 있습니다. (2022.10.22. 토요일 수정)선형 모델이 적합하지 않음을 알았으니 저희는 새로운 가설을 생각해야 합니다. 현재의 방법이 주어진 데이터에서는 적합하지 않음을 확인했으니 새로운 방법들을 찾아야 합니다. 가설은 선형 모델(z = Wx 모양)로 유지하는 방법으로 찾아보겠습니다.
이진 분류와 Sigmoid
여기서의 예시는 이진 분류(0 아님 1)이므로 0과 1 사이의 값만 나오는 함수의 모양을 따르면 될 것입니다. 이에 적합한 함수로 Sigmoid 함수가 있습니다. Sigmoid 함수가 어떤 함수인지 모르는 분들은 아래 사이트에 가서 읽어보시길 추천합니다.
시그모이드 함수 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 시그모이드 함수는 S자형 곡선 또는 시그모이드 곡선을 갖는 수학 함수이다. 시그모이드 함수의 예시로는 첫 번째 그림에 표시된 로지스틱 함수가 있으며 다음
ko.wikipedia.org
(2022.10.20.목요일 수정) 따라서 입력이 들어오면 출력은 항상 0~1 사이의 실수 값이 됩니다. 즉, 저희의 가설 함수에서 얻은 결과를 넣어서 이진 분류에 용이하게 할 수 있는 활성화 함수(activation function)로 설정할 수 있습니다.
교차 엔트로피(Cross Entropy)와 새로운 비용 함수
Sigmoid 모양을 따르는 가설 함수를 사용하면 선형 회귀 때 썼던 MSE 비용 함수를 사용하기 힘듭니다.
(2022.10.20.목요일 수정) Sigmoid 함수 y = 1 / 1 + e**-x의 그래프를 그려보면 아래와 같습니다.

그리고 Sigmoid 함수를 미분한 y'을 그려보면 아래와 같습니다.
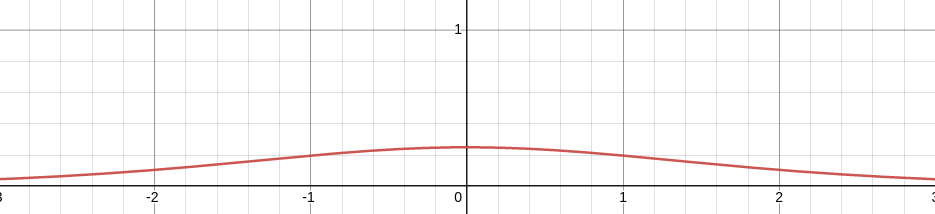
x축의 양 끝값을 보면 0에 한없이 가깝습니다. 이렇듯 sigmoid 함수처럼 s자 형태의 함수는 미분할 때 기울기 값이 사라지는 Gradient Vanishing 문제가 발생합니다. 그렇기에 미분을 통해 기울기 값을 줄여가는 방법을 적용하기가 힘듭니다. 여기서 교차 엔트로피(Cross Entropy)에 대해 알아봅시다.
교차 엔트로피는 두 확률분포가 얼마나 유사한지 실수 값으로 알 수 있는 정보입니다. 교차 엔트로피의 식은 아래와 같습니다.
H(P, Q) = -∑P(x)log(Q(x)) (P(x): 실제 확률, Q(x): 예측 확률)
이를 이용해서 비용 함수가 볼록 함수 모양을 나타낼 수 있도록 새로운 비용 함수를 정의할 수 있습니다.
cost(H(x), y) = -yln(H(x)) - (1 - y)ln(1 - H(x)) (y는 0 또는 1인 실제 값, H(x)는 가설 함수)
(2022.10.20.목요일 추가) 이제 새로운 cost 함수에서 y = 1일 때를 기준으로 그래프를 그려봅시다.

파란색 그래프가 빨간색 그래프(cost 함수)를 미분한 결과입니다. Sigmoid 함수를 미분했을 때보다는 확실히 미분 값들이 살아있음을 확인할 수 있습니다.
Multinomial Classification
지금까지는 0 또는 1로만 나누는 이진 분류의 경우를 보았습니다. 만약 3개 이상 분류해야 하는 경우는 어떻게 해야 할까요?
W = [[w1a, w1b, w1c, w1d], [w2a, w2b, w2c, w2d], [w3a, w3b, w3c, w3d]]라 하고, X = [x1, x2, x3], σ=Sigmoid라 할 때 아래의 과정을 통해 해결될 것입니다.
- X * W = [x1*w1a + x2*w2a + x3*w3a, x1*w1b + x2*w2b + x3*w3b, x1*w1c + x2*w2c + x3*w3c, x1*w1d + x2*w2d + x3*w3d]
- H(X) = 1 / (1 + e**-XW) = [σ(x1*w1a + x2*w2a + x3*w3a), σ(x1*w1b + x2*w2b + x3*w3b), σ(x1*w1c + x2*w2c + x3*w3c), σ(x1*w1d + x2*w2d + x3*w3d)

각 output 뉴런에 대한 출력은 0과 1 사이의 값을 가질 것입니다. 만약 모든 출력의 결과를 합쳐서 1이 나온다면 어느 클래스에 가장 가까운지 판별하기 좋을 것 같습니다.
Softmax와 또 새로운 비용 함수
output 뉴런으로 나온 출력들을 합쳐서 1이 되도록 할 수 있는 함수가 존재합니다. 바로 Softmax입니다. Softmax에 대한 설명은 아래 사이트에서 보시기 바랍니다.
[딥러닝] 활성화 함수 소프트맥스(Softmax)
Softmax(소프트맥스)는 입력받은 값을 출력으로 0~1사이의 값으로 모두 정규화하며 출력 값들의 총합은 항...
blog.naver.com
Softmax 식은 e**xi / ∑exj (k는 output 값들의 수, i, j는 k이하의 자연수)입니다.
예를 들어, 위의 그림의 output 뉴런 값들이 각각 [0.1, 0.24, 0.7, 0.34]라고 합시다. 이 값들을 Softmax에 넣으면 각각 [0.190707155, 0.219365444, 0.347491093, 0.242436309]이고 이 값들을 다 합치면 1이 나옵니다. 이런 특징으로 인해 Multinomial classification에서는 Softmax가, Binary classification에는 Sigmoid가 활성화 함수로 사용됩니다.
(2022.10.22. 토요일 수정)Softmax를 사용하게 되면서 크로스 엔트로피(cross-entropy) 비용 함수가 새로 등장합니다.
CrossEntropy(S, L) = -∑Li * log(Si) (S는 Softmax 결과, L은 실제 값, i는 Softmax 결과의 개수)
실제 결과를 [0, 0, 1, 0]이라 할 때, 좀 전의 softmax 결과를 크로스 엔트로피에 넣어보면
-∑Li * log(Si) = -log(0.347491093) = 0.459056323이라는 결과를 얻게 됩니다.
'개념 정리 > 머신러닝 & 딥러닝 & A.I' 카테고리의 다른 글
| 규제(Regularize) (0) | 2022.11.25 |
|---|---|
| 확률적 경사 하강(SGD) (0) | 2022.10.20 |
| 인공지능과 기계 학습 (0) | 2022.10.09 |
| CNN(Convolutional Neural Network) (0) | 2022.08.29 |
| 선형 회귀(Linear Regression) (0) | 2022.08.01 |




