| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- python3
- 운영체제
- Regression
- 파이썬
- C++
- kmu
- SQL
- 회귀
- Stack
- 정렬
- Heap
- Seq2Seq
- googleapiclient
- programmers
- 재귀
- LSTM
- instaloader
- machine learning
- Python
- 국민대
- 데이터베이스
- GIT
- PANDAS
- 국민대학교
- gan
- 스택
- 머신 러닝
- 프로그래머스
- db
- OS
- Today
- Total
정리 노트
[프로그래머스]2 x n 타일링(Python) 본문
https://school.programmers.co.kr/learn/courses/30/lessons/12900
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
이번 문제를 풀 때 모든 경우의 수를 하나하나 생각해가며 풀다 결과에 규칙이 있다는 것을 발견했습니다. 결과들이 피보나치 수열을 이루고 있었습니다!
첫 번째 풀이
피보나치 수열을 이루고 있다는 사실을 깨닫기 전에는 가로의 길이(n)가 1일 때부터 하나하나 경우의 수를 따져봤습니다.
n == 1일 경우, 가로, 세로가 (1, 2)인 직사각형 하나만 가능하므로 이때의 경우의 수는 1입니다.
n == 2일 경우, 가로, 세로가 (1, 2)인 직사각형 2개로 채우는 경우와 가로, 세로가 (2, 1)인 직사각형 2개로 채우는 경우로 이때의 경우의 수는 2입니다.
n == 3일 경우, 가로, 세로가 (1, 2)인 직사각형 3개로 채우는 경우와 가로, 세로가 (2, 1)인 직사각형을 2개를 같이 사용하는 경우가 있습니다. 모든 경우를 따져본 결과 이때의 경우의 수는 3입니다.
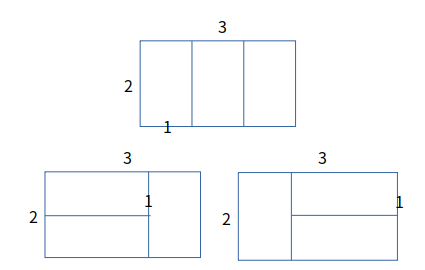
n == 4일 경우도 그림으로 하나씩 그려보면 이 때의 경우의 수는 5입니다.

이렇게 하나하나 그려보다 생각이 들었습니다. "결국 1과 2를 몇 번씩 사용하는지 세는 것 아닌가?"
길이가 n, 1의 사용 횟수를 a, 2의 사용횟수를 b라고 하면 n을 a, b에 관한 식으로 표현할 수 있습니다. n = 2 * b + a
그리고 경우의 수는 (a + b)! / (a! * b!) 로 나타낼 수 있었습니다. n에 대해 가능한 a, b쌍은 여러 개이기 때문에 각 쌍에 대해 경우의 수를 구해서 더해가는 방법으로 구하면 될 것이라 생각했습니다. 이를 파이썬으로 작성한 코드가 아래와 같습니다.
from math import factorial
def solution(n):
answer = 0
a, b = n, 0
while a >= 0:
answer += (factorial(a + b) / (factorial(a) * factorial(b)))
b += 1
a = n - 2 * b
return int(answer % 1000000007)이 코드는 프로그래머스에서 제공한 테스트 케이스에서는 무난하게 돌아갔지만 n이 1475를 넘어가면서부터 ValueError, OverflowError가 발생함을 발견했습니다.
두 번째 풀이(피보나치 수열의 등장)
다른 방법을 찾기 위해 결과들을 한 번 나열해봤습니다. 1, 2, 3, 5, 8, ... 그러다 문득 생각났습니다. "이거 피보나치 아닌가?" 해서 n이 6일 때의 경우의 수를 구해보니 13가지였고 피보나치 수열과도 일치했습니다. 바로 피보나치 수열로 풀어버렸고 아래의 코드와 같습니다.
def solution(n):
if n <= 2:
return n
a, b = 1, 2
for i in range(2, n):
a, b = b, (a + b)
return b % 1000000007프로그래머스 채점 결과 최대 28.81ms 걸렸습니다.
세 번째 풀이(더욱 빠르게)
피보나치 수열을 구현하는 내용을 찾아보다 더욱 빠른 속도로 계산이 되는 피보나치 수열을 구현하는 방법을 아래의 사이트에서 찾았습니다.
피보나치 파이썬으로 구하는 3가지 알고리즘
피보나치 파이썬 3가지 알고리즘 피보나치 수열은 아래의 수식은 만족하는 수열입니다. 바로 이전 숫자와 그 전 숫자의 합을 연속해서 구하는 수열이고 아래와 같이 진행됩니다. 이번 글에서는
myjamong.tistory.com
위 사이트의 설명대로 작성한 코드는 아래와 같습니다.
def matrix_dot(A: list, B: list):
result = [[0] * 2 for _ in range(2)]
for i in range(2):
for j in range(2):
for k in range(2):
result[i][j] += (A[i][k] * B[k][j])
return result
def matrix_pow(n: int, matrix: list):
if n == 1:
return matrix
elif n % 2 == 0:
recursive = matrix_pow(n // 2, matrix)
return matrix_dot(recursive, recursive)
else:
recursive = matrix_pow(n - 1, matrix)
return matrix_dot(recursive, matrix)
def solution(n):
A = [[1, 1], [1, 0]]
fibonacci_matrix = matrix_pow(n, A)
return fibonacci_matrix[0][0] % 1000000007프로그래머스에서 채점한 결과 최대 2.06ms 걸렸습니다.
'코딩테스트 연습' 카테고리의 다른 글
| [프로그래머스]순위 검색(Python) (0) | 2022.08.22 |
|---|---|
| [프로그래머스]두 큐 합 같게 만들기(Python) (0) | 2022.08.19 |
| [프로그래머스]뉴스 클러스터링(Python) (0) | 2022.08.12 |
| [프로그래머스]문자열 압축(Python) (0) | 2022.08.09 |
| [프로그래머스]조이스틱(Python) (0) | 2022.08.08 |
