| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- Regression
- machine learning
- Stack
- 데이터베이스
- LSTM
- db
- 프로그래머스
- programmers
- SQL
- 재귀
- Heap
- 국민대
- python3
- C++
- 운영체제
- Seq2Seq
- kmu
- 국민대학교
- googleapiclient
- Python
- 머신 러닝
- GIT
- 회귀
- OS
- 파이썬
- 스택
- PANDAS
- instaloader
- gan
- 정렬
- Today
- Total
정리 노트
[프로그래머스]조이스틱(Python) 본문
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
그동안 딥러닝이 무엇인지 계속 보다가 오랜만에 프로그래머스 코테 문제를 풀어보았습니다. 오랜만이라 그런지 문제가 어려웠습니다...
다른 사람의 풀이
그래서 결국 이번에도 다른 분의 풀이를 보며 공부했습니다.
[프로그래머스, 파이썬] 조이스틱, Greedy
[프로그래머스, 파이썬] 코딩테스트 고득점 Kit - Greedy, level 2 조이스틱
velog.io
저는 처음에 문자열 첫 번째 위치에서 왼쪽과 오른쪽 방향으로 주욱 탐색해서 계산하면 될 것이라 생각했습니다. 이렇게 생각하고 채점을 해본 결과 틀렸습니다. 왜 틀렸는지 모르겠어서 위의 글을 읽어본 결과 다른 경우도 계산해야 한다는 것을 알았습니다.
탐색할 경우의 수
- 문자열 처음부터 끝까지 순차적으로 탐색
- 문자열 처음부터 A 문자열의 왼쪽까지 탐색 후 오른쪽으로 나머지 탐색
- 문자열 마지막부터 A 문자열의 오른쪽까지 탐색 후 왼쪽으로 나머지 탐색
이에 대한 설명을 위해 예시 문자열로 "JACAAB"을 사용하겠습니다.
첫 번째인 경우 첫 번째 글자 "J"부터 "A", "C", "A", ... 순서로 하나하나 탐색하는 경우입니다.
두 번째는 처음으로 마주치는 "A" 문자열의 왼쪽 글자 "J"까지 탐색하고 마지막 문자 "B"로 넘어가서 탐색하는 경우입니다.
세 번째는 마지막 글자 "B"부터 왼쪽에서 첫 번째로 마주치는 "A" 문자열의 오른쪽 글자 "C"까지 "B", "A", "A", "C" 순서로 탐색하고 다시 "A", "A", "B"로 돌아간 다음 첫 번째 문자 "J"로 넘어가서 탐색하는 경우입니다.
이 아이디어는 "A 문자열들은 건들지 않는다"에서 출발합니다. 바꿔야 하는 이름에 A가 있으면 저희는 알파벳을 바꿀 필요가 없습니다. 그러니 커서를 A까지 옮길 필요가 없으니 A가 없는 곳으로만 커서를 움직이는 것입니다.
그림으로 나타내면 아래와 같습니다.


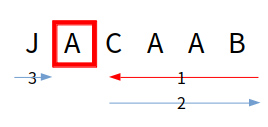
알파벳을 바꾸는 횟수의 최소값은 세 가지 탐색 방법 중 어떠한 방법이더라도 똑같습니다. 알파벳을 바꾸는 동작은 탐색과 전혀 관련이 없기 때문입니다. 따라서 알파벳을 바꾸는 최소 횟수는 항상 min(ord(char) - ord('A'), ord('Z') - ord(char) + 1) 를 따르게 됩니다.
최소 커서 이동 수 찾기
위에서 사용했던 예시를 가지고 최소 이동 수를 찾아봅시다. 시작하기 전에 커서의 최소 이동 수를 (문자열 길이) - 1로 설정하고 시작합니다. 그리고 각 반복마다 문자열을 바꾸는 횟수를 더해줍니다.
1. 첫 번째 반복(현재 커서의 인덱스 == 0)
A에서 J로 바꾸는 최소 횟수는 min(ord(char) - ord('A'), ord('Z') - ord(char) + 1)에 따라 9입니다. 그리고 문자열이 'A'가 아닌 문자열의 가장 빠른 인덱스는 2입니다. 그다음 위에서 적은 세 가지 방법 중 커서를 좌우로 가장 적게 이동하는 경우를 찾습니다.
첫 번째 방법은 문자열 처음부터 끝까지 이동하므로 (문자열 길이 == 6) - 1 == 마지막 인덱스 == 5입니다.
두 번째 방법은 처음 마주치는 A의 인덱스 '1' 전까지 오른쪽으로 탐색하다 왼쪽으로 탐색하는 경우입니다. 첫 번째 반복의 경우 현재 커서의 위치의 인덱스가 0이므로 더 이상 오른쪽으로 이동할 수 없습니다. 결국 마지막 인덱스부터 왼쪽으로 이동하는 횟수와 동일하므로
2 * (오른쪽으로 탐색한 회수 == 0) + (문자열 길이 == 6) - ( 'A'가 아닌 문자열의 가장 빠른 인덱스 == 2) == 4입니다.
세 번째 방법은 마지막 인덱스에서 인덱스 '1' 전까지 왼쪽으로 탐색하다 오른쪽으로 탐색하는 경우입니다. 따라서 커서 이동 횟수는
2 * ((문자열 길이 == 6) - ( 'A'가 아닌 문자열의 가장 빠른 인덱스 == 2)) + (현재 커서의 인덱스 == 0) == 8입니다.
5, 4, 8 중 4가 가장 적으므로 커서가 좌우로 탐색하는 가장 작은 횟수를 4로 갱신합니다.
2. 두 번째 반복(현재 커서의 인덱스 == 1)
A에서 A로 바꾸는 최소 횟수는 0입니다. 그리고 문자열이 'A'가 아닌 문자열의 가장 빠른 인덱스는 여전히 2입니다.
첫 번째 방법은 (이전 반복에서 얻은 최소 이동수) == 4입니다.
여기서 두 번째 방법의 경우, 현재 위치의 문자열이 'A'이고 그다음 문자열이 'A'가 아니기 때문에 건너뛸 문자열이 없습니다. 그래서 두 번째 경우의 횟수는 문자열의 0번째 인덱스부터 현재 커서의 인덱스까지 이동 후 반대 방향으로 이동하는 횟수와 같습니다.
2 * (현재 커서의 인덱스 == 1) + (문자열 길이 == 6) - ( 'A'가 아닌 문자열의 가장 빠른 인덱스 == 2) == 6입니다.
여기서의 세 번째 방법의 경우에도, 동일한 상황이기 때문에 커서 이동 횟수는
2 * ((문자열 길이 == 6) - ( 'A'가 아닌 문자열의 가장 빠른 인덱스 == 2)) + (현재 커서의 인덱스 == 1) == 9입니다.
4, 6, 9 중 4가 가장 적으므로 커서가 좌우로 탐색하는 가장 작은 횟수를 4로 갱신합니다.
3. 세 번째 반복(현재 커서의 인덱스 == 2)
A에서 C로 바꾸는 최소 횟수는 min(ord(char) - ord('A'), ord('Z') - ord(char) + 1)에 따라 2입니다. 그리고 문자열이 'A'가 아닌 문자열의 가장 빠른 인덱스는 5입니다. 그 다음 위에서 적은 세 가지 방법 중 커서를 좌우로 가장 적게 이동하는 경우를 찾습니다.
첫 번째 방법은 (이전 반복에서 얻은 최소 이동수) == 4입니다.
두 번째 방법은 처음 마주치는 A의 인덱스 '3' 전까지 오른쪽으로 탐색하다 왼쪽으로 탐색하는 경우입니다.
2 * (오른쪽으로 탐색한 회수 == 2) + (문자열 길이 == 6) - ( 'A'가 아닌 문자열의 가장 빠른 인덱스 == 5) == 5입니다.
세 번째 방법은 마지막 인덱스에서 인덱스 '5' 전까지 왼쪽으로 탐색하다 오른쪽으로 탐색하는 경우입니다. 현재 반복의 경우, 'A'가 아닌 문자열의 가장 빠른 인덱스가 문자열의 마지막 위치이기 때문에 왼쪽으로 탐색할 수 없습니다. 결국 문자열의 처음부터 현재 커서의 위치까지 왕복하는 횟수와 같으므로 따라서 커서 이동 횟수는
2 * ((문자열 길이 == 6) - ( 'A'가 아닌 문자열의 가장 빠른 인덱스 == 5)) + (현재 커서의 인덱스 == 2) == 4입니다.
4, 5, 4 중 4가 가장 적으므로 커서가 좌우로 탐색하는 가장 작은 횟수를 4로 갱신합니다.
위의 과정을 따라 나머지 반복을 끝내면 좌우로 최소 4번 움직일 수 있다는 것을 알 수 있습니다. 이 횟수에 알파벳을 바꾸는 횟수까지 더하면 조이스틱을 최소 16번 움직일 수 있다는 것을 얻을 수 있습니다. 지금까지의 과정을 코드로 표현한 것이 아래의 코드입니다.
def find_non_a(start: int, s: str):
current = start
while current < len(s) and s[current] == 'A':
current += 1
return current
def solution(name):
answer = 0
min_horizontal_move = len(name) - 1
for idx, char in enumerate(name):
answer += min(ord(char) - ord('A'), ord('Z') - ord(char) + 1)
next_idx = find_non_a(idx + 1, name)
min_horizontal_move = min(min_horizontal_move, 2 * idx + len(name) - next_idx, 2 * (len(name) - next_idx) + idx)
answer += min_horizontal_move
return answer
프로그래머스 채점 서버에서 확인해본 결과, 평균적으로 0.02ms, 10.2MB만큼 소모했습니다.
이번 문제 포스트는 다른 포스트들보다 상세하게 적었습니다. 왜냐 하면, 글을 마무리 짓는 지금 이 순간까지도 풀이 과정을 이해하려 했기 때문입니다. 너무 어려웠습니다....
'코딩테스트 연습' 카테고리의 다른 글
| [프로그래머스]뉴스 클러스터링(Python) (0) | 2022.08.12 |
|---|---|
| [프로그래머스]문자열 압축(Python) (0) | 2022.08.09 |
| [프로그래머스]음양 더하기(Python) (0) | 2022.07.19 |
| [프로그래머스]괄호 회전하기(Python) (0) | 2022.07.18 |
| [프로그래머스]오픈채팅방(Python) (0) | 2022.07.18 |
