| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- 프로그래머스
- Stack
- 데이터베이스
- 회귀
- Heap
- Seq2Seq
- Regression
- db
- 정렬
- 머신 러닝
- Python
- PANDAS
- gan
- 스택
- SQL
- 파이썬
- programmers
- OS
- googleapiclient
- LSTM
- python3
- 국민대학교
- kmu
- 국민대
- machine learning
- 운영체제
- 재귀
- GIT
- instaloader
- C++
- Today
- Total
정리 노트
관계 데이터 연산 - 순수 관계 연산자 본문
이 포스트는 아래의 포스트의 내용과 이어집니다.
관계 데이터 연산 - 집합 연산자
이 포스트는 국민대학교 소프트웨어학부 '데이터베이스' 강의를 듣고 요약하는 포스트입니다. 원하시는 정보가 없을 수도 있습니다. 이 점 유의 바랍니다. 오류 지적은 매우 환영합니다! 테이블
study-note-99.tistory.com
순수 관계 연산자
순수 관계 연산자에 대해 설명할 때 아래의 기호들을 사용하겠습니다.
- R : 릴레이션(테이블), R(X), X = {\( A_1, ... , A_n \)} \( \rightarrow \) R(\( A_1, ... , A_n \))
- r : R의 tuple, r \( \in \) R, r = <\( a_1, ... , a_n \)>
- \( a_i \) : r의 속성 \( A_i \)의 값, r.\(A_i\) = r[\(A_i\)] = \(a_i\)
앞으로 이야기할 연산자들은 크게 2가지로 나눌 수 있습니다.
- 근원 연산: 다른 연산으로 표현할 수 없는 연산(ex. SELECT, PROJECT, 합집합, 차집합, cartesian product)
- 복합 연산: 근원 연산으로 표현할 수 있는 연산(ex. JOIN, DIVISION, 교집합)
SELECT(\( \sigma \))
A, B가 릴레이션 R(X)의 속성들일 때, 조건식에 부합하는 R의 튜플 r의 집합이 select 연산의 결과입니다. 이를 식으로 적으면 아래와 같습니다.
$$ \sigma_{A \theta v}(R) = \{ r | r \in R \wedge r.A \theta v \} $$
$$ \sigma_{A \theta B}(R) = \{ r | r \in R \wedge r.A \theta r.B \} $$
위 식에서 \( \theta \)는 비교 연산자, v는 상수입니다. 그리고 \( r.A \theta v \), \( r.A \theta r.B \) 부분은 조건식입니다.
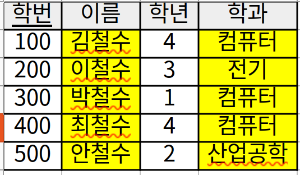
예를 들어 학생이라는 테이블이 아래의 그림처럼 있을 때, \( \sigma_{\text{학과='컴퓨터'}}(\text{학생}) \) 식의 결과는 테이블에서 노란색으로 칠해진 tuple들입니다.

여기서 전체 tuple들에 대해 select 연산에 의해 선택된 tuple들의 비율을 선택도라 합니다. SELECT 연산도 대수 연산이므로 교환 법칙이 성립합니다.
PROJECT(\( \Pi \))
릴레이션 R(X), X={\( A_1, ... , A_n \)}에서 속성 집합 Y가 R의 속성 집합 X와 Y\( \subseteq \)X, Y={\( B_1, ... , B_m \)}, n\( \geq \)m 관계일 때, R의 튜플 r에서 속성 집합 Y만을 남겨서 자른 튜플의 집합이 project 연산 결과입니다. 만약 속성 집합 Y안에 기본 키가 포함되지 않았다면 중복되는 튜플들이 생길 수 있습니다. 이 때 PROJECT 연산은 중복은 포함하지 않습니다.
이를 식으로 적으면 아래와 같습니다.
$$ \Pi_{Y}(R) = \{ <r.B_1, ..., r.B_m> | r \in R \} $$
예를 들어 학생이라는 테이블이 아래의 그림처럼 있을 때, \( \Pi_{\text{이름, 학과}}(\text{학생}) \) 식의 결과는 테이블에서 노란색으로 칠해진 tuple들(<김철수, 컴퓨터>, <이철수, 전기>, ...)입니다. 만약 이 테이블에 새로운 튜플 <600, 이철수, 1, 전기>이 삽입된다면 project 연산 결과 중복 값이 생길 수 있습니다.
JOIN(\( \Join \))
Join 연산은 'cartesian product'에 기반한 복합 연산입니다. Cartesian product 연산에 대한 설명은 아래 글에서 참고 바랍니다.
곱집합(product set / Cartesian product ) | 과학문화포털 사이언스올
과학의 모든 것, 사이언스올! 과학학습, 과학체험, 과학문화 콘텐츠 제공
www.scienceall.com
Join 연산은 theta-join(세타 조인), equi-join(동일 조인), natural join(자연 조인) 세 가지가 있습니다. 흔히 join 연산을 얘기할 때 자연 조인을 의미합니다. 이 세 가지 연산에 대해 살펴봅시다.
Theta-join, Equi-join (\( \Join \))
두 릴레이션 R(X), S(Y) (A \( \in \) X, B \(\in \) Y)에 대해 R과 S의 cartesian product 결과에서 A와 B 사이에서 \( \theta \) 조건을 만족하는 튜플들만 select 하는 연산이 theta-join 연산입니다.
$$ R \Join_{A \theta B} S = \{ r \cdot s | r \in R \wedge s \in S \wedge (r.A \theta r.B) \} = \sigma_ {A \theta B} (R \times S) $$
위에서 A와 B는 조인 속성, \( \theta \)는 연산자(<, >, =, \( \geq, \leq, \neq \) ), A \( \theta \) B는 조인 조건 식입니다.
여기서 \( \theta \) 연산자가 '='일 때의 조인을 equi-join이라 합니다.
$$ R \Join_{A = B} S = \{ r \cdot s | r \in R \wedge s \in S \wedge (r.A \theta r.B) \} = \sigma_ {A = B} (R \times S) $$
Natural join(\( \Join_{N} \))
두 릴레이션 R(X), S(Y)의 조인 속성을 Z(X \( \cap \) Y)라고 할 때 R과 S의 equi-join 결과에서 중복된 속성을 제거하는 연산이 natural join 연산입니다.
$$ \begin{align}R \Join_{N} S &= \{ <r \cdot s>[X \cup Y] | r \in R \wedge s \in S \wedge (r.Z = s.Z) \} \\ &= \Pi_ {X \cup Y} (\sigma_{Z = Z}(R \times S)) \\&= \Pi_ {X \cup Y} (R \Join_{Z = Z} S) \end{align} $$
위의 예시에서 natural join을 시행하면 아래와 같은 결과를 가집니다.

위 그림은 두 테이블을 '학과' 열을 기준으로 equi-join 한 결과와 동일합니다. 이는 두 테이블의 조인 속성이 '학과' 이기 때문에 일어난 우연입니다.
JOIN 연산의 구현
Join 연산을 프로그래밍 언어로 표현하자면, 이중 for문을 사용하는 연산입니다.
두 릴레이션 R, S를 join하려 할 때 아래의 pseudo code를 따라 진행됩니다.
(A는 R 릴레이션의 PK, S 릴레이션의 FK라는 가정)
(R을 driving table로 할 때,)
for each r \( \in \) R do
for each s \( \in \) S do
if r.A = s.A then print r \( \cdot \) s;
end;
end;
(S을 driving table로 할 때,)
for each s \( \in \) S do
for each r \( \in \) R do
if s.A = r.A then {
print r \( \cdot \) s;
break; (A는 R의 PK, 즉 unique한 값이므로 추가적으로 for문을 진행할 필요가 없음)
}
end;
end;
연산이 오래 걸리는 연산이기 때문에 driving table의 선택이 중요합니다.
DIVISION(\( \div \))
두 릴레이션 R(X), S(Y)에 대해 Y \( \subseteq \) X이고 X - Y = Z이면, R(X)는 R(Z, Y)로 표현할 수 있습니다. 따라서 division 연산은 릴레이션 R에서 Y의 tuple들을 모두 포함하는 tuple 중에서 X만을 project하는 연산입니다.
$$ R \div S = R(Z, Y) \div S(Y) = \{ t | t \in \Pi_{Z}(R) \wedge t \cdot s \in R \text{ for all } s \in S \} $$
예를 들어 '등록' 테이블과 '과목 1' 테이블이 있을 때, '등록' \( \div \) '과목 1'의 결과는 아래의 그림과 같습니다.

학번 100과 200은 과목 번호 'C312'와 'C413'을 등록하지 않았고, 학번 500은 'C312'만 만족하므로 divison 연산 결과에 포함되지 않습니다. 학번 300과 400에서 'C312'와 'C413'이 모두 등장하므로 두 학번이 division 연산 결과에 나오게 됩니다. X = {학번, 과목 번호}, Y ={과목 번호} 일 때, Z = X - Y = {학번}이므로 학번만 출력됩니다.
참고로 이 연산은 SQL에서 제공하지 않습니다.
작명 연산(\( \rho \))
지금까지의 4가지 연산 외에도 자주 쓰이는 연산입니다. 이 연산은 복잡한 관계 대수식에서 중간 결과 릴레이션에 이름을 붙이거나 그 릴레이션의 속성 이름을 변경할 때 사용합니다.
- \( \rho_{S} \)(E): 관계 대수식 E의 결과 릴레이션을 S라 부르고 저장
- \( \rho_{S(B_{1}, B_{2}, ..., B_{m})} \)(E): 관계 대수식 E의 결과 릴레이션의 이름을 S라 하고, 속성 이름들을 \( B_{1}, B_{2}, ..., B_{m} \)로 수정해 저장
'개념 정리 > 데이터베이스' 카테고리의 다른 글
| [MySQL]SELECT문 (2) | 2024.02.08 |
|---|---|
| 관계 데이터 연산 - 확장된 관계 연산자 (0) | 2023.11.07 |
| 관계 데이터 연산 - 집합 연산자 (0) | 2023.09.13 |
| 관계 데이터 구조 (0) | 2023.08.10 |
| 논리적 데이터 모델링 (0) | 2023.07.24 |



