| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- machine learning
- 국민대학교
- SQL
- PANDAS
- gan
- Stack
- Heap
- 파이썬
- kmu
- 회귀
- python3
- 정렬
- OS
- 재귀
- programmers
- 머신 러닝
- Seq2Seq
- 프로그래머스
- 운영체제
- 국민대
- googleapiclient
- db
- GIT
- C++
- Python
- LSTM
- Regression
- 데이터베이스
- instaloader
- 스택
- Today
- Total
정리 노트
문자열 패턴 찾기(with DFA) 본문
이번 글에서는 DFA(Determistic Finite State of Automaton)을 이용해 문자열 안에서 특정 패턴을 찾는 방법에 대해 적어보겠습니다.
Naive 한 방법
DFA로 들어가기 전에 왜 DFA를 써야 하는지 느끼기 위해 naive 하게 찾는 방법부터 보겠습니다. 예를 들어 문자열 "BLUERED"이 있고, 여기서 패턴 "RED"을 찾는 문제를 푼다고 합시다.

RED를 찾는 가장 naive 한 방법은 하나하나 다 살펴보는 것입니다.

이렇게 하나하나 체크해서 패턴을 찾을 수 있습니다. 하지만 이렇게 찾는다면 시간이 오래 걸립니다. 문자열의 길이를 N, 패턴의 길이를 M이라고 한다면, time complexity는 O(NM)이라 표현할 수 있습니다. 그리고 이러한 방법은 매번 불일치가 일어날 때마다 roll-back이 일어나기 때문에 텍스트가 stream의 형태로 들어오는 경우에 사용할 수 없습니다.

이 roll back을 없애기 위해 DFA, KMP 알고리즘 등을 사용해서 문자열에서 패턴을 찾게 되는 것입니다.
DFA(Deterministic Finite State Automaton)
DFA는 유한한 개수의 상태(state, start(시작)와 accept(끝)까지 포함)들과 각 상태에서의 transition들로 이루어져 있습니다. 문자열로 DFA 구성할 경우, 하나의 char당 오직 하나의 transition만 존재합니다. 예를 들어 패턴 "ABABACA"로 DFA를 아래와 같이 그릴 수 있습니다.
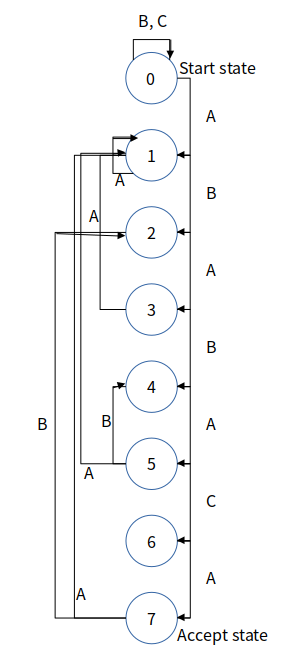
0번 state(Start state)부터 시작해서 어떤 문자를 입력받았는지에 따라 다른 state로 이동합니다. 이 그림에서는 0이 아닌 state에서 0번 state로 가는 transition은 생략했습니다. 실제로도 이렇게 생략해서 그리는 DFA도 있습니다. state의 number는 현재까지 패턴 문자들이 몇 개 일치했는지를 알려줍니다. 예를 들어, 현재 3번 state라는 것은 지금까지 3개가 패턴과 일치했다는 것을 의미합니다.
7번 state(Accept state)로 이동하게 되면 패턴("ABABACA")을 순서대로 입력받았다는 뜻으로 사용자가 입력으로 준 문자열 안에서 이 패턴을 찾았다는 것이 됩니다.
이러한 DFA 그림을 이차원 배열로 표현할 수 있습니다.
| char \ state | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| A | 1 | 1 | 3 | 1 | 5 | 1 | 7 | 1 |
| B | 0 | 2 | 0 | 4 | 0 | 4 | 0 | 2 |
| C | 0 | 0 | 0 | 0 | 0 | 6 | 0 | 0 |
| Others | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
이차원 배열의 각 원소는 현재 state에서 char 입력을 받으면 어느 state로 이동해야 하는지 알려줍니다. 예를 들어, 5번 state에서 'A'를 받으면 1번 state, 'B'를 받으면 4번, 'C'를 받으면 6번, 나머지 문자들을 받으면 0번으로 이동합니다.
사용자의 입력 텍스트가 "ACABABACA"라고 하고, 이 텍스트로 DFA를 돌려봅시다. 이때의 state 번호를 나열해보겠습니다.
| A | C | A | B | A | B | A | C | A | |
| 0 | 1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
7번 state가 됐을 때, 이때의 (텍스트 인덱스 - 7(패턴의 길이)) 값이 저희가 찾는 패턴의 시작 인덱스가 됩니다. 위의 예시인 경우, 텍스트의 인덱스 9번에서 accept state가 됐으므로 인덱스 2번에서 패턴이 시작됨을 알 수 있습니다.
DFA 만들기
이제 패턴 "ABABACA"에 대해서 DFA를 어떻게 만들지에 대해 알아봅시다. DFA를 만들기 위해 다음과 같은 가정을 하나 합시다.
j번 state에서 transition을 그리려 할 때, 0번 ~ j - 1번 state는 모두 만들어졌다고 가정
5번 state(j == 5)에서 문자에 대한 transition을 그려봅시다.

먼저, 문자 C를 받으면(char 'c' == pattern[5]) state가 6번으로 넘어가야 한다는 건 확실합니다.

문제는 문자가 C가 아닐 경우입니다. 생각해보기 위해 다시 naive 한 알고리즘으로 탐색할 때를 생각해봅시다.

패턴과 맞지 않은 문자가 발견됐기 때문에 roll-back이 일어날 것입니다.

여기서 빨간 선으로 묶은 부분을 주목해봅시다. 빨간색으로 묶은 "BABA"는 패턴의 1번 인덱스 ~ (j - 1) 번 인덱스와 똑같습니다. 따라서 이 과정은 패턴의 1번~(j - 1) 번 인덱스까지의 내용을 DFA에 0번 state부터 돌리는 것과 같게 됩니다. "BABA"를 DFA에 돌려서 얻은 state를 X(X == 3)라고 합시다. 그럼 DFA에서는 X에서 mismatch 났던 문자 'B'를 입력받았을 때 이동할 state로 이동하게 될 것입니다. 이 state에 j번 state에서 문자 'B'를 받았을 때의 transition을 연결하면 됩니다. Mismatch 났던 문자가 A였다면, X state에서 A 입력을 받을 때 이동할 state로 transition을 연결하면 됩니다.

이 과정을 표로 확인해봅시다.
| char \ state | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| A | 1 | 1 | 3 | 1 | 5 | ? | ? | ? |
| B | 0 | 2 | 0 | 4 | 0 | ? | ? | ? |
| C | 0 | 0 | 0 | 0 | 0 | 6 | ? | ? |
| Others | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
즉, 표['A'][5] = 표['A'][3] = 1이 되고, 표['B'][5] = 표['B'][3] = 4가 됩니다. 이를 일반화시켜서 작성하면 아래와 같이 됩니다.
표[mismatched character][j] = 표[mismatched character][X]
이 과정에서는 X state를 찾기 위해 j번의 step이 필요합니다. J번의 step 소요를 줄이기 위해 X state를 계속 유지시켜 상수만큼의 시간이 걸리게 할 수 있습니다.
X state 유지하기
위의 과정을 통해 j번째 state에서의 transition을 다 완성해서 이제 j + 1번째의 transition을 그린다고 합시다. 이때의 새로운 X state(X')이 어떻게 변하는지를 봅시다.
j가 하나 늘어났으므로 DFA에서 1번 ~ j번 인덱스까지의 pattern 내용("BABAC")을 돌립니다. 그러면, X'은 0이 됩니다. DFA에서 흘러간 과정을 잘 보시면 X' = 표['C'][X]라는 사실을 알 수 있습니다. 따라서 X'을 구하기 위해 j번의 step이 아닌 1번의 인덱싱을 통해 얻을 수 있게 됩니다.
DFA 만드는 c++ 코드
// 실제로 동작하지 않을 코드입니다. 흐름 참고용으로만 봐주세요.
// 사용자의 입력과 패턴이 A, B, C로만 이루어졌다고 가정
// dfaTable: DFA를 이차원 배열로 표현, 정수형 원소 저장
void constructDFATable(string pattern)
{
// 초기화
for (int i = 0; i < 4; i++) { dfaTable[i][0] = 0; }
dfaTable[convert(pattern[0])][0] = 1; // convert(): 문자에 해당하는 행 번호로 변환
for (int X = 0, j = 1; j <= pattern.length(); j++)
{
// 글에서 dfaTable[mismatched character][j] = dfaTable[mismatched character][X] 임을 소개
for (int k = 0; k < 4; k++) { dfaTable[k][j] = dfaTable[k][X]; }
if (j == pattern.length()) break; // 생성 종료
dfaTable[convert(pattern[j])][j] = j + 1;
X = dfaTable[convert(pattern[j])][X];
}
}DFA를 만들 때, 시간 복잡도와 공간 복잡도 모두 O(R(사용자가 입력한 텍스트에서 사용된 문자의 종류 수) * M(패턴 길이))입니다.
DFA 사용할 때의 복잡도
DFA를 이용해서 문자열 안에서 패턴을 찾는 알고리즘을 실행하면 O(M(패턴 길이) + N(사용자가 입력한 문자열 길이)) 만큼 걸립니다.
int matchPattern(string usrInput, string pattern)
{
// usrInput 안에 pattern이 있으면 pattern이 시작하는 인덱스 리턴하는 함수
// pattern이 usrInput 안에 없으면 -1 반환
int usrInputIdx, patternIdx; usrInputIdx = patternIdx = 0;
while (usrInputIdx < usrInput.length() && patternIdx < pattern.length())
{
patternIdx = dfaTable[convert(usrInput[usrInputIdx])][patternIdx];
usrInputIdx++;
}
if (usrInputIdx < usrInput.length()) return usrInputIdx - patternIdx;
else return -1;
}Naive 한 알고리즘을 사용했을 때보다 더 빠르게 패턴을 찾을 수 있다는 것을 알 수 있습니다.
'개념 정리 > 알고리즘' 카테고리의 다른 글
| Flajolet-Martin (1) | 2023.06.13 |
|---|---|
| DGIM (0) | 2023.06.12 |
| Heap 정렬(Heap Sort) - Heap 정렬하기 (0) | 2022.12.11 |
| Heap 정렬(Heap Sort) - Heap 만들기 (0) | 2022.12.10 |
| 백트래킹(Backtracking) (0) | 2022.11.13 |



