| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- kmu
- 정렬
- programmers
- gan
- Stack
- 재귀
- machine learning
- PANDAS
- Python
- 프로그래머스
- 데이터베이스
- db
- 스택
- C++
- googleapiclient
- 운영체제
- python3
- Regression
- Seq2Seq
- 국민대학교
- 파이썬
- 머신 러닝
- Heap
- 국민대
- GIT
- instaloader
- 회귀
- OS
- LSTM
- SQL
- Today
- Total
정리 노트
Comb Sort 본문
이번 포스트도 버블 정렬에 대해 알고 있다는 가정 하에 작성되었습니다. 버블 정렬을 모르시는 분들은 제가 전에 적었던 글을 참고하시기 바랍니다.
2022.09.05 - [알고리즘] - 버블 정렬(Bubble sort)
Comb Sort
2022.09.06 - [알고리즘] - 칵테일 셰이커 정렬(Cocktail Shaker Sort) 에서 적었듯이 기존 버블 정렬에는 아쉬운 점이 있었습니다. 크기가 작은 데이터가 배열의 끝에 위치한 경우 제 위치로 찾아가기까지 오래 걸렸습니다. Comb Sort는 이 문제점을 개선한 정렬 알고리즘입니다.
Gap
기존 버블 정렬에서는 등장하지 않았던 'gap'이 등장합니다. gap은 현재 데이터와 swap 할 데이터 간의 거리를 의미합니다. 즉 버블 정렬에서는 gap이 1이었던 것입니다.
처음에 gap의 크기를 1보다 큰 값으로 설정하고 점차 gap을 1까지 줄여가며 정렬을 진행합니다. 주로 shrink factor(k)만큼 줄이고, gap은 (배열의 길이) / k (소수점 버림)로 시작해서 1까지 k씩 나눠가며 감소시킵니다. 많은 사람들의 시행 결과 k값은 1.3으로 권장되고 있습니다.
정렬 과정
길이가 5인 정수형 배열({4, 2, 5, 2, 1})를 정렬해본다고 합시다. 그러면 초기의 gap은 5 / 1.3 -> 3으로 설정합니다. 그럼 첫 번째 comb sort는 아래의 그림처럼 진행됩니다.
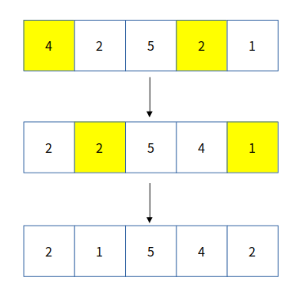
첫 번째 원소인 '4'와 3만큼 떨어진 '2'와 비교 연산을 실행합니다. 앞의 원소가 뒤의 원소보다 크므로 swap이 발생합니다. 다음 원소 '2'는 3만큼 떨어진 '5'와 비교 연산을 실행합니다. 앞의 원소가 뒤의 원소보다 작으므로 swap은 발생하지 않습니다. '1'에서 3만큼 떨어지면 배열의 길이를 벗어나므로 첫 번째 pass를 종료합니다.
다음 pass로 넘어가기 전에 gap을 5 / 1.3 / 1.3 -> 2로 설정합니다. 그러면 다음 pass에서는 아래의 그림처럼 정렬이 일어납니다.

첫 번째 원소인 '2'와 2만큼 떨어진 '5'와 비교 연산을 실행합니다. 앞의 원소가 뒤의 원소보다 작으므로 swap은 발생하지 않습니다. 다음 원소 '1'일 때에도 swap은 발생하지 않습니다. '5'일 때도 동일합니다. 이 이상은 배열의 길이를 벗어나므로 두 번째 pass를 종료합니다.
세 번째 pass를 위해 gap을 계산하면 5 / 1.3 / 1.3 / 1.3 -> 2로 전의 gap과 동일하므로 넘어가겠습니다.
네 번째 pass에서 사용될 gap 값은 5 / 1.3 / 1.3 / 1.3 / 1.3 -> 1입니다. 즉 기존의 버블 정렬과 동일하게 진행될 것입니다.
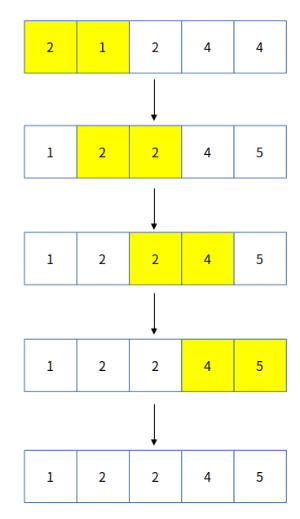
네 번째 pass 종료 후, gap이 1이었으므로 이제 배열이 정렬될 때까지 계속 bubble sort를 진행시킵니다. 하지만 위의 예제에서는 이미 배열이 정렬되었으므로 4번의 비교 연산 후 bubble sort가 종료됩니다.
Comb Sort C++ 코드
Comb sort를 c++로 구현하면 아래와 같습니다.
#include <iostream>
using namespace std;
void combSort(int[], int);
int main()
{
int myArray[5] = {4, 2, 5, 2, 1};
combSort(myArray, 5);
return 0;
}
void combSort(int arr[], int n)
{
int gap = n / 1.3;
bool sorted = false;
while (!sorted)
{
if (gap <= 1)
{
gap = 1;
sorted = true;
}
for (int i = 0; i + gap < n; i++)
{
if (arr[i] > arr[i + gap])
{
swap(arr[i], arr[i + gap]);
sorted = false;
}
}
gap /= 1.3;
}
}Comb Sort도 bubble sort나 cocktail shaker sort와 동일하게 메모리 복잡도는 O(1)이라 할 수 있습니다. 위에 작성한 코드를 보면 사용한 변수는 gap, sorted, i 등 사용될 변수의 개수가 정해져 있습니다. 그리고 기존의 배열 안에서 정렬이 일어나므로 In-place 알고리즘입니다.
하지만 Comb Sort는 Non-stable sorting 알고리즘입니다. 즉 정렬 전의 순서가 정렬 후에도 똑같지 않다는 것입니다. 위의 예시로 썼던 배열을 생각해봅시다. 정렬하기 전에는 원소 '2'가 2개 있었고 각각 인덱스 1과 3에 위치했습니다. 하지만 모든 정렬 과정이 끝나고 인덱스 1의 2는 인덱스 3으로 옮겨졌고 인덱스 3의 2는 인덱스 2로 옮겨졌습니다. 앞뒤가 바뀌었습니다. 만약 stable 한 알고리즘이었다면 앞뒤가 유지되었을 것입니다. 인덱스 1의 2가 인덱스 1에, 인덱스 3의 2가 인덱스 2 같이 앞에 있던 원소는 그대로 앞에 있는 게 유지됐어야 stable 한 알고리즘입니다.
비교 연산 횟수 비교
여기서 gap 계산은 코드에서 사용한 계산법을 사용하겠습니다. 위의 예시로 들었던 배열을 기존의 bubble sort로 정렬시켰다면 비교 연산 횟수는 5 * 4 / 2 = 10회, comb sort로 정렬시키면 2 + 3 + 4 + 4 = 13회로 비교 횟수는 bubble sort가 더 적게 합니다. 하지만 이는 길이가 적은 배열일 때만 그렇지 배열의 길이가 길어질수록 comb sort에서의 비교 횟수가 훨씬 적습니다. 만약 배열의 길이가 100인 역으로 정렬된 배열을 정렬한다고 하면 bubble sort에서는 100 * 99 / 2 = 4950회, comb sort에서는 24 + 42 + 56 + 67 + 75 + 81 + 86 + 90 + 93 + 95 + 94 + 95 + 97 + 98 + 99 + 99 = 1102회로 훨씬 적은 비교 연산을 실행합니다.
'개념 정리 > 알고리즘' 카테고리의 다른 글
| Shell Sort (0) | 2022.09.13 |
|---|---|
| 삽입 정렬(Insertion Sort) (0) | 2022.09.12 |
| 선택 정렬(Selection Sort) (0) | 2022.09.10 |
| 칵테일 쉐이커 정렬(Cocktail Shaker Sort) (0) | 2022.09.06 |
| 버블 정렬(Bubble sort) (0) | 2022.09.05 |




