| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- SQL
- C++
- Regression
- 회귀
- 정렬
- 파이썬
- 스택
- Python
- machine learning
- OS
- 운영체제
- 프로그래머스
- LSTM
- googleapiclient
- 국민대학교
- GIT
- db
- 재귀
- 국민대
- 머신 러닝
- python3
- kmu
- Heap
- instaloader
- 데이터베이스
- Stack
- programmers
- PANDAS
- gan
- Seq2Seq
- Today
- Total
정리 노트
[BDA X 이지스 퍼블리싱]5주차 스터디 요약 본문
이 포스트는 BDA와 이지스 퍼블리싱에서 같이 진행하는 Easy Study 5주 차 내용을 요약하는 포스트입니다.
아래의 도서가 스터디에 사용한 교재입니다.
http://www.easyspub.co.kr/20_Menu/BookView/B001/607/PUB
www.easyspub.co.kr
K-평균 군집화(K-Means Clustering) 모델
K-평균 군집화 모델은 특정 데이터와 이 데이터가 속한 군집의 중심점까지의 거리의 제곱을 최소화하는 K개의 군집을 찾는 비지도 학습 모델입니다.
군집화에 사용되는 알고리즘으로 로이드(Lloyd) 알고리즘과 엘칸(Elkan) 알고리즘이 있습니다. 가장 기본적인 로이드 알고리즘은 아래의 흐름으로 진행됩니다.
- K개의 중심점을 임의로 선택
- 각 데이터 샘플마다 가장 가까운 중심을 해당 샘플을 포함한 군집의 중심으로 지정
- 군집 별로 평균을 계산해 새 중심으로 갱신
- 중심이 변하지 않을 때까지 1 ~ 3번 반복
여기서 엘칸 알고리즘은 거리를 직접적으로 계산하지 않고, 삼각 부등식을 활용해 거리의 상한선과 하한선을 만들어 진행합니다. 이 방식은 거리를 정확히 계산하는 것보다 계산량이 적은 것으로 알려져 있습니다. 추가적인 엘칸 알고리즘 설명은 다음의 사이트를 참고하시기 바랍니다.( https://www.cse.iitd.ac.in/~rjaiswal/2015/col870/Project/Nipun.pdf )
하지만 이 군집화 알고리즘이 항상 전역 최적값을 보장하는 것은 아닙니다. 아래의 그림처럼 로컬 최적화에 빠져 사람이 기대하는 만큼의 군집화 성능을 보이지 않을 때도 존재합니다.

sklearn.cluster.KMeans
sklearn 패키지에서 K-평균 군집화 클래스 API를 제공하므로 이를 사용해 간단하게 K-평균 군집화 모델을 만들어 학습시킬 수 있습니다.
from sklearn.cluster import KMeans
import numpy as np
x = np.array([[1, 2], [1, 4], [1, 0], [10, 2], [10, 4], [10, 0]])
kmeans = KMeans(n_clusters=2, random_state=0).fit(x)
print(f"샘플별 군집 번호:", kmeans.labels_)
# 샘플별 군집 번호: [1 1 1 0 0 0]클래스의 파라미터에 대해 설명하면 아래와 같습니다.
| 파라미터 | 주요값 | 기본값 | 의미 |
| n_cluster | int > 0 | 8 | 생성할 군집 수 |
| init | 'k-means++' / 'random' | 'k-means++' | 중심점 초기화 방법 |
| algorithm | 'lloyd' / 'elkan' | 'lloyd' | 학습 알고리즘 |
sklearn.cluster.KMeans
Examples using sklearn.cluster.KMeans: Release Highlights for scikit-learn 1.1 Release Highlights for scikit-learn 0.23 A demo of K-Means clustering on the handwritten digits data Bisecting K-Means...
scikit-learn.org
계층적 군집화(Hierarchical Clustering) 모델
데이터를 계층적 구조로 조직화하는 데 사용하는 알고리즘으로 데이터들을 유사성 또는 거리 기준에 따라 여러 레벨의 군집으로 구성하는 방법입니다.
여기서 사용하는 군집 사이의 거리는 여러 방법으로 계산할 수 있습니다.
- 단일 연결법(single/minimum linkage): 두 군집 간의 데이터끼리의 모든 거리를 비교해 최소 거리로 정의
- 최장 연결법(complete/maximum linkage): 두 군집 간의 데이터끼리의 모든 거리를 비교해 최대 거리로 정의
- 중심 연결법(centroid linkage): 각 군집의 중심을 계산해 중심 사이의 거리로 정의
- 와드 연결법(ward linkage): 두 군집을 합칠 때 분산의 증가분을 거리로 정의
일반적으로 와드 연결법이 가장 좋은 전략이라 알려져 있다고 합니다.
알고리즘을 코드로 작성하자면 아래와 같습니다.
import numpy as np
def get_distance(a, b):
distance = np.inf
for a_point in a:
for b_point in b:
point_distance = np.linalg.norm(a_point - b_point)
if point_distance < distance: distance = point_distance
return distance여기서는 단일 연결법으로 두 군집 간의 거리를 정의합니다.
x = np.array([[1, 0], [1, 3], [0, 1], [4, 9], [3, -2], [-1, 1]])
clusters = [[x[i]] for i in range(len(x))]
print("초기 군집:", clusters)
while len(clusters) > 1:
value = np.inf
index1, index2 = -1, -1
for i in range(len(clusters)):
for j in range(i):
dist = get_distance(clusters[i], clusters[j])
if dist < value:
value = dist
index1, index2 = i, j
cluster1 = clusters.pop(index1)
cluster2 = clusters.pop(index2)
clusters.append(cluster1 + cluster2)
print(f"단계 {6 - len(clusters)}: {clusters}")while문을 실행할 때마다 가장 가깝게 있는 두 군집이 하나의 군집으로 합쳐집니다.
sklearn.cluster.AgglomerativeClustering
sklearn 패키지에서 계층적 군집화 클래스 API를 제공하므로 이를 사용해 간단하게 계층적 군집화 모델을 만들어 학습시킬 수 있습니다.
from sklearn.cluster import AgglomerativeClustering
import numpy as np
x = np.array([[1, 2], [1, 4], [1, 0], [4, 2], [4, 4], [4, 0]])
clustering1 = AgglomerativeClustering(n_clusters=2, linkage='complete').fit(x)
print(f"군집 수 설정한 모델링 결과: {clustering1.labels_}")
clustering2 = AgglomerativeClustering(n_clusters=None, linkage='complete', distance_threshold=2.5).fit(x)
print(f"군집화 기준 거리 설정한 모델링 결과: {clustering2.labels_}")클래스의 파라미터에 대해 설명하면 아래와 같습니다.
| 파라미터 | 주요값 | 기본값 | 의미 |
| n_clusters | int>0 / None | 2 | 생성할 군집 수 |
| linkage | 'ward' / 'complete' / 'average' / 'single' | 'ward' | 연결법(군집 사이 거리 기준) 선택 |
| affinity | 'euclidian' / 'l1' / 'l2' / 'manhattan' / 'cosine' / 'precomputed' | 'euclidian' | 거리 계산 방법 선택 |
| distance_threshold | None / float>0 | None | 군집화 기준 거리 설정 |
sklearn.cluster.AgglomerativeClustering
Examples using sklearn.cluster.AgglomerativeClustering: A demo of structured Ward hierarchical clustering on an image of coins Agglomerative clustering with and without structure Agglomerative clus...
scikit-learn.org
주 성분 분석(PCA) 모델
데이터의 차원이 커질수록 sparsity가 급격히 증가하는 차원의 저주가 발생합니다. 따라서 필요 없는 차원의 수를 줄이는 것이 중요합니다. 이럴 때 사용하는 방법 중 하나가 PCA입니다.
PCA는 차원 축소를 위한 비지도 학습 모델로 기존 데이터의 정보를 최대한 훼손하지 않도록 차원을 축소하는 방식입니다.
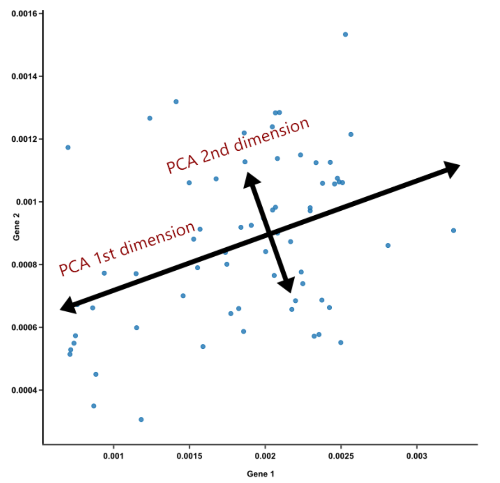
먼저 원래 데이터 공간에서 사영했을 때 분산이 가장 커지는 축(첫 번째 주성분 축)을 하나 찾습니다. 그다음 첫 번째 축과 수직인 공간 중에서 사영시킬 때 분산이 가장 커지는 축(두 번째 주성분 축)을 찾습니다. 이 과정을 필요한 주성분 수만큼 반복해서 PCA를 진행합니다.
sklearn.decomposition.PCA
from sklearn.datasets import load_digits
from sklearn.decomposition import PCA
x, y = load_digits(return_X_y=True)
pca = PCA(random_state=1234)
pca.fit(x)클래스의 파라미터에 대해 설명하면 아래와 같습니다.
| 파라미터 | 주요값 | 기본값 | 의미 |
| n_components | None / int / 0 < float < 1 / 'mle' | None | 추출할 주성분 수 |
| svd_solver | 'full' / 'arpack' / 'randomized' / 'auto' | 'auto' | 최적화 알고리즘 선택 |
sklearn.decomposition.PCA
Examples using sklearn.decomposition.PCA: A demo of K-Means clustering on the handwritten digits data Principal Component Regression vs Partial Least Squares Regression The Iris Dataset Blind sourc...
scikit-learn.org
