| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- LSTM
- kmu
- 국민대
- Stack
- programmers
- gan
- Seq2Seq
- 회귀
- Regression
- googleapiclient
- instaloader
- python3
- OS
- GIT
- C++
- 운영체제
- Heap
- PANDAS
- Python
- 국민대학교
- 머신 러닝
- SQL
- 스택
- 정렬
- 프로그래머스
- 재귀
- 데이터베이스
- 파이썬
- machine learning
- db
- Today
- Total
정리 노트
Local Sensitive Hashing for Cosine Similarity 본문
이 포스트는 국민대학교 소프트웨어학부 '빅데이터최신기술' 강의를 듣고 요약하는 포스트입니다. 원하시는 정보가 없을 수도 있습니다. 이 점 유의 바랍니다. 오류 지적은 매우 환영합니다!
이전의 포스트에서 자카드 유사도로 문서 간의 유사도를 계산했고, LSH(Local Sensitive Hashing)를 통해 탐색 속도를 높였습니다.
유사도를 계산할 때 코사인 유사도를 사용한다면, LSH도 이에 맞게 바뀌어야 합니다. 코사인 유사도에 대한 설명은 제가 저번에 적었던 포스트의 마지막 부분을 참고하시면 됩니다.
따라서 이번 포스트에서 코사인 유사도를 사용할 때 LSH가 어떻게 이루어지는지 알아보겠습니다.
Bag of Words
알아보기 전에 문서를 표현했던 방법에 대해 다시 한번 봅시다. 이전 포스트에서처럼 문서를 집합으로 표현하면 하나의 문서 안에서 같은 단어가 여러 번 나와도 그 단어의 등장 횟수는 1입니다. Bag of words 모델을 사용하면 같은 단어가 여러 번 나오면 여러 번 나온 횟수를 저장합니다. 이를 통해 집합으로만 표현했던 문서를 아래와 같이 벡터(다중 집합)로 표현할 수 있게 되고, 유사도를 계산할 때 코사인 유사도를 사용할 수 있게 됩니다. 쉽게 그림으로 표현하기 위해 2차원 벡터로 표현하겠습니다.
| 등장한 문자(단어) | A | B |
| 문서 1 | 3 | 5 |
| 문서 2 | 6 | 2 |
| 문서 3 | 5 | 2 |
| 문서 4 | 4 | 6 |
| 문서 5 | 2 | 2 |
Hyperplane for LSH
이전에 LSH를 한 것처럼 하려면 코사인 유사도가 비슷한 벡터들의 해시 값이 동일해야 합니다. 그래야 유사한 문서들끼리 그룹이 지어지고, 질의 문서가 탐색해야 할 대상을 줄일 수 있습니다.
위를 만족하는 해시 함수가 여러 가지 있겠지만 많이 사용하는 것은 hyperplane입니다. 아래의 블로그에서 hyperplane에 대해 쉽게 설명하고 있으니 확인하시면 좋습니다.
초평면 (Hyperplane)
초평면이란? 초평면에 '초'는 뛰어넘다(초) 입니다. 평면을 뛰어넘은 평면이라는 뜻인데요. 평면에서 더 확장된 개념이라는걸 이름에서도 알 수 있습니다. 두개의 변수로 만들어진 1차식은 아래
hsm-edu-math.tistory.com
임의의 hyperplane을 생성하면 벡터들을 hyperplane을 기준으로 두 그룹으로 나눌 수 있습니다. 예를 들어 위의 예시로 작성한 두 개의 문서를 임의의 hyperplane을 사용해 나눌 수 있습니다. 여기서 hyperplane을 기준으로 왼쪽을 0, 오른쪽을 1로 지칭할 수 있습니다. 그러면 문서 1, 4는 영역 0, 문서 2, 3, 5는 영역 1에 속한다고 얘기할 수 있습니다.
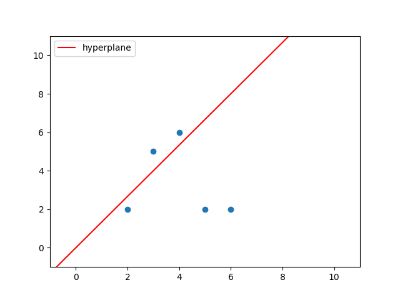
Hyperplane을 여러 개 만들수록 벡터가 존재하는 영역을 더 자세히 표현할 수 있습니다. 아래처럼 세 개의 hyperplane을 사용하면, 한 개를 사용할 때보다 벡터의 위치를 더 자세히 특정할 수 있습니다. 즉 벡터의 signature를 아래와 같이 표현할 수 있게 됩니다.

| hyperplane 1 | hyperplane 2 | hyperplane 3 | |
| 문서 1의 signature | 0 | 1 | 0 |
| 문서 2의 signature | 1 | 1 | 1 |
| 문서 3의 signature | 1 | 1 | 1 |
| 문서 4의 signature | 0 | 1 | 0 |
| 문서 5의 signature | 1 | 0 | 0 |
Signature를 만들면, 동일한 signature끼리 그룹을 만들 수 있습니다. 여기서는 문서 1과 4로 그룹을 만들고, 2와 3으로 그룹을 만들게 됩니다.
그리고 질의 문서의 signature와 동일한(또는 hamming distance가 가까운) signature를 가지는 문서들을 대상으로 탐색할 수 있게 됩니다. 해밍 거리에 대한 설명은 아래의 글을 참고하시길 바랍니다.
해밍 거리 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 블록 부호 이론에서, 해밍 거리(Hamming距離, 영어: Hamming distance)는 곱집합 위에 정의되는 거리 함수이다. 대략, 같은 길이의 두 문자열에서, 같은 위치에서 서로
ko.wikipedia.org
LSH for Cosine Similarity에 대한 가벼운 분석
- 두 벡터의 각이 \(\theta\) 일 때, 임의의 hyperplane의 같은 영역에 있을 확률: \(1 - {\theta \over \pi}\)
- Hyperplane의 수를 k라 할 때, 생성할 수 있는 그룹의 수: \(2^k\)
- 벡터(문서)의 수를 n이라 할 때, 평균 그룹 크기: \(n \over 2^k\)
- 해밍 거리가 d 이하인 그룹의 수: \(\Sigma_{i=0}^d {k \choose i}\)
- 해밍 거리가 d 이하인 벡터(문서) 수의 평균: \({n \over 2^k}{\Sigma_{i=0}^d {k \choose i}}\)
Hyperplane이 만약 \(\theta\) 안을(두 벡터 사이를) 통과한다면 두 벡터는 서로 다른 영역에 있게 됩니다. 즉, 같은 영역에 있으려면 hyperplane이 \(\theta\) 밖에 있어야 합니다. 따라서 확률은 \({\pi - \theta} \over \pi\) = \(1 - {\theta \over \pi}\)입니다.
위의 5가지를 통해 다음의 확률을 계산할 수 있습니다.
각이 \(\theta\)인 두 벡터의 signature의 해밍 거리가 d 이하일 확률(=탐색에 성공할 확률)
이는 다음과 같이 계산됩니다.
$$ \Sigma_{i=0}^d {k \choose i} \cdot \left( 1 - {\theta \over \pi} \right)^{k - i} \cdot \left( {\theta \over \pi} \right)^i $$
위 식을 쉽게 설명하자면 아래와 같습니다.
- Hyperplane의 수를 늘리면(공간을 더 잘게 나누면) 탐색 속도는 향상되지만, 정확도는 떨어진다.
- 허용하는 hamming distance가 클수록(더 많은 곳을 탐색하면) 정확도는 오르지만, 탐색 속도는 떨어진다.
- Hyperplane 수와 허용하는 hamming 거리 둘 다 늘리면 탐색 대상 벡터 수 대비 정확도가 오르지만, hamming 거리를 계산하는 overhead가 증가한다.
'개념 정리' 카테고리의 다른 글
| Bloom Filters (0) | 2023.06.13 |
|---|---|
| Reservoir Sampling (0) | 2023.06.11 |
| Locality Sensitive Hashing (1) | 2023.06.09 |
| Min-Hashing (1) | 2023.06.08 |
| Amazon Cognito (0) | 2023.02.22 |
